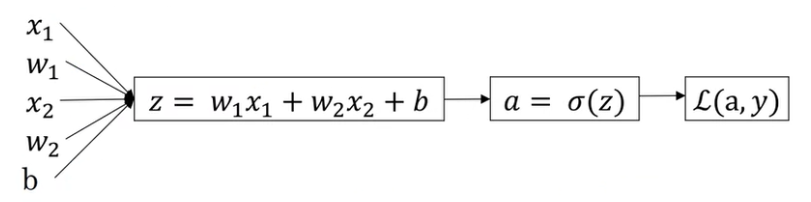
全连接神经网络(无框架)

这一节我认为是原博客作者的代码实战中最精华的一部分，建议跟着敲一遍。正如本文开头所说，不会详细介绍神经网络、激活函数和损失函数的表达式，都是直接丢公式的。中间可能会穿插一些原理介绍，小标题写为简单的理论分析。

无框架单层单神经元（逻辑回归）分类

这是一个很粗糙的项目，代码不规范，但是很清楚的展示了深度学习项目的流程，没有怎么写过python代码的可以看一看。本节完成的是一个猫狗分类任务

逻辑回归的公式描述

逻辑回归是一个学习算法，用于对真值只有0或1的“逻辑”问题进行建模。给定输入,逻辑回归输出一个。这个是对真值的一个估计。

方法也很简单，就是将数据经过一个线性变换后输入非线性映射函数（sigmoid）输出概率，公式如下

上面这个公式就是我们的模型，模型有两个可学习参数：w和b。其本质上是只有一个神经元的神经网络。

逻辑回归名字叫回归，看描述其实能知道他并不是一个处理回归问题的算法，而是一个处理分类问题的算法，其输出为真的概率，我们可以根据这个概率进行分类。一般对于分类任务（或者说涉及对概率进行建模的任务）我们会使用交叉熵作为误差函数。公式如下

误差函数是定义在每个样本上的，而损失函数是定义在整个样本上的，表示所有样本误差的“总和”。这个“总和”其实就是平均值，即损失函数𝐽(𝑤,𝑏)为:

简单的理论分析（梯度下降、链式法则、计算图）

接下来就是根据损失函数，使用梯度下降法优化我们的模型。在我的理解里，梯度下降法有效是建立在以下事实和观察上的

我们希望损失函数越小越好
我们发现损失函数的自变量沿梯度反方向变化可以使损失函数变小，
公式给出的损失函数自变量（y）不是w和b，调整他们没有用
y可以表示为w和b，w和b也可以是损失函数的自变量，w和b沿梯度反方向变化可以使损失函数变小

当然直接把w和b带入损失函数公式求梯度，但是如果中间的变化再复杂一点，这种做法显然是不适合计算机编程的，更合适的方法是使用链式法则逐级求解梯度。

我们用肉眼看这个神经网络，可以很清楚的看到这个梯度是怎样传递的，但是机器怎么知道呢？一般机器是通过建立计算图来记录这个链式规则的，就像我们在编译原理里语法分析的时候需要建立语法树一样。比如上面的逻辑回归，假设我们的数据是二维的，其计算图如下

计算图的每一个节点应该只包含原子运算，方便链式过程进行追踪和求导。

我们在实现的时候就不实现计算图的代码了，就根据上面的链式过程求一下导数
$$

$$
上面是具体的单个二维数据样本求导过程。一般我们处理数据是一批一批处理的。对于一批数据，预测结果为,其求导就涉及到矩阵的求导了，这里直接给出结论

代码

所有的代码都不是我写的，原出处，我只是抄下来自己巩固复习一下

下面是数据集的介绍

说起最经典的二分类任务，大家都会想起小猫分类（或许跟吴恩达老师的课比较流行有关）。在这个项目中，我也顺应潮流，选择了一个猫狗数据集（https://www.kaggle.com/datasets/fusicfenta/cat-and-dog?resource=download ）。

在此数据集中，数据是按以下结构存储的：

基础知识中已经提到一个深度学习任务包含六个步骤。首先进行数据预处理。

input_shape=(224, 224)
def load_dataset(dir, data_num):
    cat_images = glob(osp.join(dir, 'cats', '*.jpg'))
    dog_images = glob(osp.join(dir, 'dogs', '*.jpg'))
    cat_tensor = []
    dog_tensor = []

    for idx, image in enumerate(cat_images):
        if idx >= data_num:
            break
        i = cv2.imread(image) / 255
        i = cv2.resize(i, input_shape)
        cat_tensor.append(i)

    for idx, image in enumerate(dog_images):
        if idx >= data_num:
            break
        i = cv2.imread(image) / 255
        i = cv2.resize(i, input_shape)
        dog_tensor.append(i)

    X = cat_tensor + dog_tensor
    Y = [1] * len(cat_tensor) + [0] * len(dog_tensor)
    X_Y = list(zip(X, Y))
    shuffle(X_Y)
    X, Y = zip(*X_Y)
    return X, Y

def generate_data(dir='data/archive/dataset', input_shape=(224, 224)):
    train_X, train_Y = load_dataset(osp.join(dir, 'training_set'), 400)
    test_X, test_Y = load_dataset(osp.join(dir, 'test_set'), 100)
    return train_X, train_Y, test_X, test_Y

load_dataset从dir中读取data_num张狗和data_num张猫，读入图片时将其颜色范围归一化到[-1,1]的范围内，然后resize为224*224。这里归一化的方法是将颜色值除以255。第24_{26行代码在保证X}、Y对应的情况下打乱样本顺序。generate_data从不同的文件夹中读取训练集和测试集。

接下来定义网络结构。根据

我们只需要设置一个w向量一个b向量即可。推理函数如下

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def predict(w, b, X):
    return sigmoid(np.dot(w.T, X) + b)

但是显然这样做的话一张图片应该用一个向量表示，所以对训练集和测试集还要处理一下

def resize_input(a: np.ndarray):
    h, w, c = a.shape
    a.resize((h * w * c))
    return a
train_X, train_Y, test_X, test_Y = generate_data()

train_X = [resize_input(x) for x in train_X]
test_X = [resize_input(x) for x in test_X]
train_X = np.array(train_X).T
train_Y = np.array(train_Y)
train_Y = train_Y.reshape((1, -1))
test_X = np.array(test_X).T
test_Y = np.array(test_Y)
test_Y = test_Y.reshape((1, -1))

接下来定义损失函数，直接敲公式

def loss(y_hat, y):
    return np.mean(-(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)))

接下来应该是定义优化策略，我们目前只提到了最基础的梯度下降，就是计算梯度然后回传误差，下面这个函数并不是一个典型的定义优化策略的步骤，他其实是一整步的训练流程，包括前向传播（3、4行）梯度计算（5、6、7行）和梯度回传（第8行）

def train_step(w, b, X, Y, lr):
    m = X.shape[1]
    Z = np.dot(w.T, X) + b
    A = sigmoid(Z)
    d_Z = A - Y
    d_w = np.dot(X, d_Z.T) / m
    d_b = np.mean(d_Z)
    return w - lr * d_w, b - lr * d_b

完成的训练流程代码如下

def init_weights(n_x=224 * 224 * 3):
    w = np.zeros((n_x, 1))
    b = 0.0
    return w, b
    
def train(train_X, train_Y, step=1000, learning_rate=0.00001):
    w, b = init_weights()
    print(f'learning rate: {learning_rate}')
    for i in range(step):
        w, b = train_step(w, b, train_X, train_Y, learning_rate)

        # 输出当前训练进度
        if i % 10 == 0:
            y_hat = predict(w, b, train_X)
            ls = loss(y_hat, train_Y)
            print(f'step {i} loss: {ls}')
    return w, b

最后是测试代码，其实就是预测一下测试集，算一下准确率

def test(w, b, test_X, test_Y):
    y_hat = predict(w, b, test_X)
    predicts = np.where(y_hat > 0.5, 1, 0)
    score = np.mean(np.where(predicts == test_Y, 1, 0))
    print(f'Accuracy: {score}')

上面的代码再加上一些必要的库文件就可以跑了。原文作者跑出来的精度是很拉的，最好都到不了0.6，基本相当于瞎蒙。首先这个网络确实是太简陋了，只有一个神经元，无法对猫狗分类任务准确建模（后面会加深神经网络的层数）；其次我们的训练方法也过于纯真，很难发挥神经网络真正的威力（后面会引入更多学习技巧）；最后这个网络将图片直接展平为向量破坏了像素间的位置关系，神经网络很难学习到有价值的信息，哪怕加上更多的神经元也必然有其瓶颈（后面会引入CNN和Transformer）；

无框架深度神经网络分类任务

这一节将神经网络的层数增多，并将代码规范化。

深度神经网络的训练流程

设神经网络层数为，用上标表示某一层网络的参数或激活函数，为输入(为输入层，为输出)，为激活函数，前向传播过程为

反向传播过程为

注意上面虽然写了,但是更新参数并不是立马执行的，后续梯度计算依赖的是老的W和b

显然反向传播时会使用到正向传播过程中的一些值，所以需要将其缓存下来（这也是为什么训练神经网络的时候会消耗大量的显存，因为中间有大量的中间变量）

通用分类器类以及工具函数

首先定义通用分类器类，注释写的很清楚，就不过多分析了

class BaseRegressionModel(metaclass=abc.ABCMeta):

    def __init__(self):
        pass

	#前向过程，可以用于测试，也可以用于训练，train_mode区分
    #训练时需要缓存变量
    def forward(self, X: np.ndarray, train_mode=True) -> np.ndarray:
        pass

	#反向传播函数，缓存梯度
    def backward(self, Y: np.ndarray) -> np.ndarray:
        pass

	#原始梯度下降法更新参数，后面这个函数会改为调用通用的优化器更新参数
    def gradient_descent(self, learning_rate: float) -> np.ndarray:
        pass

	#保存模型
    def save(self, filename: str):
        pass

	#加载模型
    def load(self, filename: str):
        pass
	#计算损失
    def loss(self, Y: np.ndarray, Y_hat: np.ndarray) -> np.ndarray:
        return np.mean(-(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)))
	#训练集上评估模型
    def evaluate(self, X: np.ndarray, Y: np.ndarray, return_loss=False):
        Y_hat = self.forward(X, train_mode=False)
        Y_hat_predict = np.where(Y_hat > 0.5, 1, 0)
        accuracy = np.mean(np.where(Y_hat_predict == Y, 1, 0))
        if return_loss:
            loss = self.loss(Y, Y_hat)
            return accuracy, loss
        else:
            return accuracy

工具函数主要是提高激活函数泛用性，这个是放在工具包里的，纯属原作者炫技（bushi

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_de(x):
    tmp = sigmoid(x)
    return tmp * (1 - tmp)

def relu(x):
    return np.maximum(x, 0)

def relu_de(x):
    return np.where(x > 0, 1, 0)

def get_activation_func(name):
    if name == 'sigmoid':
        return sigmoid
    elif name == 'relu':
        return relu
    else:
        raise KeyError(f'No such activavtion function {name}')


def get_activation_de_func(name):
    if name == 'sigmoid':
        return sigmoid_de
    elif name == 'relu':
        return relu_de
    else:
        raise KeyError(f'No such activavtion function {name}')

代码

深度神经网络继承自基础分类器，构造函数中初始化层数（num_layer）、每层神经元数（neuron_cnt，列表）、每一层权重矩阵(W，列表)和偏移向量(b列表)以及激活函数。这里w采用了参数随机初始化（算一下梯度就知道w一开始是不能全部为一样的值的，这样无法训练），行列数与输入输出有关，实在想不清楚就自己纸上写两个矩阵比划一下。最后设置缓存列表，可以看到缓存列表占用空间比模型自身参数占用空间还要大，处理模型参数的梯度缓存，还有中间变量。

class DeepNetwork(BaseRegressionModel):
	def __init__(self, neuron_cnt: List[int], activation_func: List[str]):
        assert len(neuron_cnt) - 1 == len(activation_func)
        self.num_layer = len(neuron_cnt) - 1
        self.neuron_cnt = neuron_cnt
        self.activation_func = activation_func
        self.W: List[np.ndarray] = []
        self.b: List[np.ndarray] = []
        for i in range(self.num_layer):
            self.W.append(
                np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) * 0.2)
            self.b.append(np.zeros((neuron_cnt[i + 1], 1)))
        self.Z_cache = [None] * self.num_layer
        self.A_cache = [None] * (self.num_layer + 1)
        self.dW_cache = [None] * self.num_layer
        self.db_cache = [None] * self.num_layer

前向传播主要就是抄公式，同时参照下面注释缓存变量,注意W和b本来模型就有，不用缓存

def forward(self, X, train_mode=True):
    if train_mode:
        self.m = X.shape[1]
    A = X
    self.A_cache[0] = A
    for i in range(self.num_layer):
        Z = np.dot(self.W[i], A) + self.b[i]
        A = get_activation_func(self.activation_func[i])(Z)
        if train_mode:
            self.Z_cache[i] = Z
            self.A_cache[i + 1] = A
    return A

反向传播也是抄公式，注意这里缓存了梯度，而不是直接更新参数

def backward(self, Y):
    dA = -Y / self.A_cache[-1] + (1 - Y) / (1 - self.A_cache[-1])
    assert (self.m == Y.shape[1])

    for i in range(self.num_layer - 1, -1, -1):
        dZ = dA * get_activation_de_func(self.activation_func[i])(
            self.Z_cache[i])
        dW = np.dot(dZ, self.A_cache[i].T) / self.m
        db = np.mean(dZ, axis=1, keepdims=True)
        dA = np.dot(self.W[i].T, dZ)
        self.dW_cache[i] = dW
        self.db_cache[i] = db

然后是优化策略，这里也就是梯度下降

def gradient_descent(self, learning_rate):
    for i in range(self.num_layer):
        self.W[i] -= learning_rate * self.dW_cache[i]
        self.b[i] -= learning_rate * self.db_cache[i]

存取模型使用numpy的savez方法存取键值对

def save(self, filename: str):
    save_dict = {}
    for i in range(len(self.W)):
        save_dict['W' + str(i)] = self.W[i]
    for i in range(len(self.b)):
        save_dict['b' + str(i)] = self.b[i]
    np.savez(filename, **save_dict)

def load(self, filename: str):
    params = np.load(filename)
    for i in range(len(self.W)):
        self.W[i] = params['W' + str(i)]
    for i in range(len(self.b)):
        self.b[i] = params['b' + str(i)]

写到这里，模型代码就写好了。不过之前说的第一步还没有做，就是数据预处理。代码原作者github有，这里就懒得贴了，反正就是上一节代码的基础上把图片直接处理成向量了。不过我看他是没有打乱数据的。当然按目前这个实现方法打不打乱是无所谓的，毕竟所有的数据都送进神经网络学习了。

根据作者的实验结果，这个模型的准确率是不如逻辑回归的。虽然说越大的模型理论上来说建模能力应该更强，但是要达到这个理论性能，是需要一定的训练技巧的。

无框架深度神经网络分类任务+优化器

这一节将介绍多种优化手段，并在上一节的基础上加上优化器，将代码完善为类pytorch代码

改进机器学习的基本方法

注意，本小节介绍的方法都不是通用方法，而是当碰到某些问题的时候才会使用，所以这些方法不会出现在后面的分类代码中。但是这些方法确实是经常使用的，在pytorch里就是调用一个函数的事情，所以介绍一下。

我们可以将神经网络表现不好的原因归为两类，一是欠拟合，二是过拟合。

欠拟合一般表现为在训练集上的误差很大，解决的方法是增加模型的复杂度，或者增加训练时间

当然也可以改进模型结构，但是能不能改出来就各凭本事了，这里讨论的是一般的解决方法

过拟合一般表现为训练集和验证集上的表现差距大，训练集上表现效果好但是验证集表现效果差。过拟合的解决方法是增加训练数据（更严谨的说法是应该是优化训练集数据分布）以及正则化

如果训练集和验证集上表现效果都很好，但是测试集上表现效果很差，说明数据集划分不行，现在公开的数据集几乎不可能出现这种情况。注意这里说的是表现差距大，有差距是正常的，不是说验证集上掉了一点点分就过拟合了
另外不要杠训练集上效果差验证集上效果好属于什么，属于你模型没训练，结果是模型瞎给的，刚好碰上了

训练神经网络都是基于梯度下降法，而对于深层的神经网络，使用链式法则（计算图）进行梯度计算会面临梯度的消失或者爆炸的问题（就是传递过程中系数越乘越小或者越乘越大）。梯度问题一般使用加权初始化并在训练过程中检查梯度的方法解决。

为了让梯度下降法更加顺利，我们应该尽可能让每一层神经网络的输入向量更加规整，这种方法称为归一化。

这里主要介绍正则化、参数初始化以及归一化，因为这两个东西是写代码会用到的。梯度检查这里不介绍了，有兴趣可以看看原文。

正则化

正则化说白了就是向给损失函数添加一些与参数有关的额外项，用来防止过拟合，添加的项称为正则项。比如原始逻辑回归的损失函数为，为了训练更加平滑，我们可以增加一个和参数相关的项，将损失函数修改为

加的这一项是的L2范数，即所有分量的平方求和。增加这一项之后，参数的更新方式如下

此时w的系数变为了，参数会倾向于变得更小，相当于减少了参数对网络的影响，简化了网络的描述的函数的复杂程度，从而产生减轻过拟合的效果。

上面使用L2正则化的方法又称为权重衰减，是一种较为通用的正则化方法，pytorch等框架提供了接口用以控制权重衰减系数。

还有一种常用的通用正则化方法叫dropout，其做法是在训练过程中按照一定的概率使某一部分神经元不参与计算，其目的也是为了不然神经网络拟合的函数过于复杂以至于过拟合。pytorch中有dropout层，可以适当丢弃某一层神经网络的一些输出。

还有一些其他的正则化方法，例如数据增强、提前停止，甚至根据具体任务设置具体的正则项等等，这里就不过多介绍。

归一化

使输入向量的每一个分量都尽量满足正态分布，称为归一化。当然这里的输入不一定使整个神经网络的输入，每一层的输入也可以归一化，前者称为输入归一化，后者称为批归一化（批是什么后面会说）。

使输入满足正态分布的做法也很简单，就是计算一下输入的均值和方差，然后将输入减去均值除以方差即可。当然有的时候我们也不希望每一层的输入都是正态分布，我们在得到符合正态分布的输入后，在添加适当的均值和方差让网络学习一个适当的分布。归一化可以看作是一个神经网络层，pytorch框架中提供了可直接调用的normolization层，并且提供了在不同尺度上（比如批、元素、通道等）归一化的选项

参数初始化

参数初始化是为了减轻梯度弥散或者梯度爆炸等问题而提出的，其做法是给初始矩阵赋予特定的值。具体怎么赋值已经有很多研究了，pytorch中也提供了一系列的初始化方法

改进梯度下降法

这一节很重要，大家在pytorch代码中看到的优化器其实就是这一节介绍的方法的实现。不过这一节也不是说大家都得会手搓一个优化器什么的，原作者这里说的很好，本节技术“会用”一般要优先于“会写”。

batch

前面的代码在进行梯度下降时使用整个训练集的平均梯度来更新模型参数，即一次训练过程为

for i in range(m):
    calculate_gradient_average()
gradient_descent()

m为总样本大小。当训练集过大时，这样做显然是不合适的，遍历整个数据集要花很长时间，梯度下降的速度将十分缓慢。

其实，我们不一定要等遍历完了整个数据集再做梯度下降。相较于每次遍历完所有m个训练样本再更新，我们可以遍历完一小批次(mini-batch)的样本就更新。即

for i in range(m / batch_size)
  for j in range(batch_size):
      calculate_gradient_average()
  gradient_descent()

现在的梯度下降法每进行一次内层循环，就更新一次参数。我们还是把一次内层循环称为一个step，一次外层循环称为一个epoch。注意这里两端代码我就是意思一下，因为实际代码里不存在遍历每一个样本的循环，别和前面或者后面真正能跑的代码对应着看。

不难理解，当batch_size为整个样本大小时，分批梯度下降就变为整体梯度下降，梯度下降会很平滑，对显存要求也比较大，梯度下降的速度较慢；当batch_size为1时，分批梯度下降就变为随机梯度下降，即每计算一个样本就更新一次梯度，对显存要求最小，但是梯度变化会很大，甚至可能不收敛。所以batch_size 需要选择一个合适的值。一般情况下都会将batch_size设为2的幂。

高级梯度更新方法

原始的梯度更新就是沿着梯度反方向更新参数，以下山为例，就是沿着最陡的方向往下滑，这样滑肯定是速度最快的，但是我们的最终目标是滑到山下时间最短，当山的地形很复杂时，直接沿梯度反方向滑速度虽然快但是路程不一定最短，甚至可能狠狠绕圈子，如下图蓝线所示

为了解决这个问题，在梯度更新时我们不仅应该考虑当前梯度，还要考虑之前的综合梯度，之前的综合梯度能够代表一个下降的势头，可以一定程度上纠正当前梯度。如何考虑综合梯度呢，就是通过下面的方法

TCP的RTT计算也是用的这种方法，称为指数加权移动平均数，这里的记录了之前梯度的指数加权平均数，代表了梯度下降的“势头”，称为动量(Momentun)，使用动量修正后的梯度下降如红色所示。

但看指数加权移动平均的递推公式好像没什么问题，权重加起来刚好为1，但是你从第一项开始写，不难发现第一项由于没有之前的值，的，这样权重和不就不对了吗，正确的做法需要对结果进行修正。不过还是那句话，本节知识主要是会用，就不纠结这些代码细节了。

在一个神经网络中，不同的参数需要的更新幅度可能不一样。但是，在默认情况下，所有参数的更新幅度都是一样的（即学习率）。为了平衡各个参数的更新幅度，RMSProp(Root Mean Squared Propagation) 在参数更新公式中添加了一个和参数大小相关的权重S。与 Momentum 类似，RMSProp使用了某种移动平均值来平滑这个权重的更新。其梯度下降公式如下：

而咱深度学习中最常用的优化方式，Adam，其实就是Momentum 与 RMSProp 的结合版，就是对每一个参数的更新既考虑了动量，又考虑了不同的学习率

学习率衰减

训练时的学习率不应该是一成不变的。在优化刚开始时，参数离最优值还差很远，选较大的学习率能加快学习速度。但是，经过了一段时间的学习后，参数离最优值已经比较近了。这时，较大的学习率可能会让参数错过最优值。因此，在训练一段时间后，减小学习率往往能够加快网络的收敛速度。这种训练一段时间后减小学习率的方法叫做学习率衰减。

学习率衰减是一条启发性的规则。我们可以有意识地在训练中后期调小学习率，也可以直接用框架提供的学习率衰减策略

代码

读取数据集的代码这里放一下，没什么说的，就是读图片，不过注意这个默认参数，按照作者的写法，本质上是读取了2*train_size和2*test_size张图片，其实也就是前面的data_num，这里起个名字叫train_size有点歧义

import os
from typing import Tuple

import cv2
import numpy as np


def load_set(data_path: str, cnt: int, img_shape):
    cat_dirs = sorted(os.listdir(os.path.join(data_path, 'cats')))
    dog_dirs = sorted(os.listdir(os.path.join(data_path, 'dogs')))
    images = []
    for i, cat_dir in enumerate(cat_dirs):
        if i >= cnt:
            break
        name = os.path.join(data_path, 'cats', cat_dir)
        cat = cv2.imread(name)
        images.append(cat)

    for i, dog_dir in enumerate(dog_dirs):
        if i >= cnt:
            break
        name = os.path.join(data_path, 'dogs', dog_dir)
        dog = cv2.imread(name)
        images.append(dog)

    for i in range(len(images)):
        images[i] = cv2.resize(images[i], img_shape)
        images[i] = np.reshape(images[i], (-1))
        images[i] = images[i].astype(np.float32) / 255.0

    return np.array(images)


def get_cat_set(
    data_root: str,
    img_shape: Tuple[int, int] = (224, 224),
    train_size=1000,
    test_size=200,
) -> Tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray]:

    train_X = load_set(os.path.join(data_root, 'training_set'), train_size,
                       img_shape)
    test_X = load_set(os.path.join(data_root, 'test_set'), test_size,
                      img_shape)

    train_Y = np.array([1] * train_size + [0] * train_size)
    test_Y = np.array([1] * test_size + [0] * test_size)

    return train_X.T, np.expand_dims(train_Y,
                                     0), test_X.T, np.expand_dims(test_Y.T, 0)

本节将二分类模型抽象类修改为

class BaseRegressionModel(metaclass=abc.ABCMeta):

    def __init__(self):
        pass


    def forward(self, X: np.ndarray, train_mode=True) -> np.ndarray:
        pass


    def backward(self, Y: np.ndarray) -> np.ndarray:
        pass


    def get_grad_dict(self) -> Dict[str, np.ndarray]:
        pass


    def save(self) -> Dict[str, np.ndarray]:
        pass


    def load(self, state_dict: Dict[str, np.ndarray]):
        pass

    def loss(self, Y: np.ndarray, Y_hat: np.ndarray) -> np.ndarray:
        return np.mean(-(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)))

    def evaluate(self, X: np.ndarray, Y: np.ndarray, return_loss=False):
        Y_hat = self.forward(X, train_mode=False)
        Y_hat_predict = np.where(Y_hat > 0.5, 1, 0)
        accuracy = np.mean(np.where(Y_hat_predict == Y, 1, 0))
        if return_loss:
            loss = self.loss(Y, Y_hat)
            return accuracy, loss
        else:
            return accuracy

这段代码和上一节的区别在于将gradient_descent改为get_grad_dict，这里只是获得模型梯度，梯度下降算法放在单独的优化器类内使用

具体神经网络设计与上一节几乎一致,区别主要有以下几点

参数初始化方法，使用He Initialization初始化W矩阵。这个初始化方法pytorch里内置了，至于具体怎么操作的就看代码吧
get_grad_dict不做梯度下降，单纯的把梯度包装成一个矩阵返回
save和load不是保存到文件或读取文件，而是返回一个字典或者读取一个字典
train中做了batch划分
训练流程有一点改变，具体看122行到131行
画了loss图，别觉得土，不用tensorboard的话loss图还真是真么画的

class DeepNetwork(BaseRegressionModel):

    def __init__(self, neuron_cnt: List[int], activation_func: List[str]):
        super().__init__()
        assert len(neuron_cnt) - 1 == len(activation_func)
        self.num_layer = len(neuron_cnt) - 1
        self.neuron_cnt = neuron_cnt
        self.activation_func = activation_func
        self.W: List[np.ndarray] = []
        self.b: List[np.ndarray] = []
        for i in range(self.num_layer):
            self.W.append(
                np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) *
                np.sqrt(2 / neuron_cnt[i]))
            self.b.append(np.zeros((neuron_cnt[i + 1], 1)))

        self.Z_cache = [None] * self.num_layer
        self.A_cache = [None] * (self.num_layer + 1)
        self.dW_cache = [None] * self.num_layer
        self.db_cache = [None] * self.num_layer

    def forward(self, X, train_mode=True):
        if train_mode:
            self.m = X.shape[1]
        A = X
        self.A_cache[0] = A
        for i in range(self.num_layer):
            Z = np.dot(self.W[i], A) + self.b[i]
            A = get_activation_func(self.activation_func[i])(Z)
            if train_mode:
                self.Z_cache[i] = Z
                self.A_cache[i + 1] = A
        return A

    def backward(self, Y):
        # Assume the activation of the lat layer is sigmoid
        assert self.activation_func[-1] == 'sigmoid' and \
            self.neuron_cnt[-1] == 1
        assert (self.m == Y.shape[1])

        dA = 0
        for i in range(self.num_layer - 1, -1, -1):
            if i == self.num_layer - 1:
                dZ = self.A_cache[-1] - Y
            else:
                dZ = dA * get_activation_de_func(self.activation_func[i])(
                    self.Z_cache[i])
            dW = np.dot(dZ, self.A_cache[i].T) / self.m
            db = np.mean(dZ, axis=1, keepdims=True)
            dA = np.dot(self.W[i].T, dZ)
            self.dW_cache[i] = dW
            self.db_cache[i] = db

    def get_grad_dict(self) -> Dict[str, np.ndarray]:
        grad_dict = {}
        for i in range(len(self.dW_cache)):
            grad_dict['W' + str(i)] = self.dW_cache[i]
        for i in range(len(self.db_cache)):
            grad_dict['b' + str(i)] = self.db_cache[i]
        return grad_dict

    def save(self) -> Dict[str, np.ndarray]:
        param_dict = {}
        for i in range(len(self.W)):
            param_dict['W' + str(i)] = self.W[i]
        for i in range(len(self.b)):
            param_dict['b' + str(i)] = self.b[i]
        return param_dict

    def load(self, state_dict: Dict[str, np.ndarray]):
        for i in range(len(self.W)):
            self.W[i] = state_dict['W' + str(i)]
        for i in range(len(self.b)):
            self.b[i] = state_dict['b' + str(i)]


def save_state_dict(model: BaseRegressionModel, optimizer: BaseOptimizer,
                    filename: str):
    state_dict = {'model': model.save(), 'optimizer': optimizer.save()}
    np.savez(filename, **state_dict)


def load_state_dict(model: BaseRegressionModel, optimizer: BaseOptimizer,
                    filename: str):
    state_dict = np.load(filename)
    model.load(state_dict['model'])
    optimizer.load(state_dict['optimizer'])


def train(model: BaseRegressionModel,
          optimizer: BaseOptimizer,
          X,
          Y,
          total_epoch,
          batch_size,
          model_name: str = 'model',
          save_dir: str = 'work_dirs',
          recover_from: Optional[str] = None,
          print_interval: int = 100,
          dev_X=None,
          dev_Y=None,
          plot_mini_batch: bool = False):
    if recover_from:
        load_state_dict(model, optimizer, recover_from)
    m = X.shape[1]
    indices = np.random.permutation(m)
    shuffle_X = X[:, indices]
    shuffle_Y = Y[:, indices]
    num_mini_batch = math.ceil(m / batch_size)
    mini_batch_XYs = []
    for i in range(num_mini_batch):
        if i == num_mini_batch - 1:
            mini_batch_X = shuffle_X[:, i * batch_size:]
            mini_batch_Y = shuffle_Y[:, i * batch_size:]
        else:
            mini_batch_X = shuffle_X[:, i * batch_size:(i + 1) * batch_size]
            mini_batch_Y = shuffle_Y[:, i * batch_size:(i + 1) * batch_size]
        mini_batch_XYs.append((mini_batch_X, mini_batch_Y))
    print(f'Num mini-batch: {num_mini_batch}')

    mini_batch_loss_list = []
    for e in range(total_epoch):
        for mini_batch_X, mini_batch_Y in mini_batch_XYs:
            mini_batch_Y_hat = model.forward(mini_batch_X)
            model.backward(mini_batch_Y)
            optimizer.zero_grad()
            optimizer.add_grad(model.get_grad_dict())
            optimizer.step()
            if plot_mini_batch:
                loss = model.loss(mini_batch_Y, mini_batch_Y_hat)
                mini_batch_loss_list.append(loss)

        currrent_epoch = optimizer.epoch

        if currrent_epoch % print_interval == 0:
            # save_state_dict(
            #     model, optimizer,
            #     os.path.join(save_dir, f'{model_name}_{currrent_epoch}.npz'))
            accuracy, loss = model.evaluate(X, Y, return_loss=True)
            print(f'Epoch: {currrent_epoch}')
            print(f'Train loss: {loss}')
            print(f'Train accuracy: {accuracy}')
            if dev_X is not None and dev_Y is not None:
                accuracy, loss = model.evaluate(dev_X, dev_Y, return_loss=True)
                print(f'Dev loss: {loss}')
                print(f'Dev accuracy: {accuracy}')

        optimizer.increase_epoch()

    save_state_dict(model, optimizer,
                    os.path.join(save_dir, f'{model_name}_latest.npz'))

    if plot_mini_batch:
        plot_length = len(mini_batch_loss_list)
        plot_x = np.linspace(0, plot_length, plot_length)
        plot_y = np.array(mini_batch_loss_list)
        plt.plot(plot_x, plot_y)
        plt.show()

为了方便观看，我们将训练代码122_{131单独拉出来}

for e in range(total_epoch):
    for mini_batch_X, mini_batch_Y in mini_batch_XYs:
        mini_batch_Y_hat = model.forward(mini_batch_X)
        model.backward(mini_batch_Y)
        optimizer.zero_grad()
        optimizer.add_grad(model.get_grad_dict())
        optimizer.step()

    currrent_epoch = optimizer.epoch

    if currrent_epoch % print_interval == 0:
        # print loss
        ...
     optimizer.increase_epoch()
save_state_dict(model, optimizer, os.path.join(save_dir, f'{model_name}_latest.npz'))

在一个epoch中，对每一个batch，走一遍前向反向，得到梯度，然后就是优化器的操作了。优化器首先将上一步保存的梯度清零，然后读取本次梯度，然后优化模型。所以接下来我们看优化器的代码

首先是抽象基类，抽象基类需要三个参数，分别是神经网络参数、初始学习率和学习率衰减策略。注意神经网络参数self.param_dict是一个直接赋值，修改他就是修改神经网络参数。这个优化器基类实现了以下功能：

维护当前的epoch和step，以辅助其他参数的计算。
维护当前的学习率，并通过使用_lr_scheduler的方式支持学习率衰减。
定义了从词典中保存/读取优化器的方法save, load。
定义了维护的梯度的清空梯度方法zero_grad和新增梯度方法add_grad。不难发现，具体的优化器子类应该是需要维护self.grad_dict变量的
允许子类实现step方法，以使用不同策略更新参数。

class BaseOptimizer(metaclass=abc.ABCMeta):

    def __init__(
            self,
            param_dict: Dict[str, np.ndarray],
            learning_rate: float,
            lr_scheduler: Callable[[float, int], float] = const_lr) -> None:
        self.param_dict = param_dict
        self._epoch = 0
        self._num_step = 0
        self._learning_rate_zero = learning_rate
        self._lr_scheduler = lr_scheduler


    def epoch(self) -> int:
        return self._epoch


    def learning_rate(self) -> float:
        return self._lr_scheduler(self._learning_rate_zero, self.epoch)

    def increase_epoch(self):
        self._epoch += 1

    def save(self) -> Dict:
        return {'epoch': self._epoch, 'num_step': self._num_step}

    def load(self, state_dict: Dict):
        self._epoch = state_dict['epoch']
        self._num_step = state_dict['num_step']

    def zero_grad(self):
        for k in self.grad_dict:
            self.grad_dict[k] = 0

    def add_grad(self, grad_dict: Dict[str, np.ndarray]):
        for k in self.grad_dict:
            self.grad_dict[k] += grad_dict[k]


    def step(self):
        pass

接下来是几个具体的优化器实现，不多说了，看注释吧

#朴素梯度下降法，额外维护了一个self.grad_dict
class GradientDescent(BaseOptimizer):
    def __init__(self, param_dict: Dict[str, np.ndarray],
                 learning_rate: float) -> None:
        super().__init__(param_dict, learning_rate)
        self.grad_dict = deepcopy(self.param_dict)

    def save(self) -> Dict:
        return super().save()

    def load(self, state_dict: Dict):
        super().load(state_dict)

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.param_dict[k] -= self.learning_rate * self.grad_dict[k]

# 动量梯度下降法，额外维护了梯度字典、动量权重以及动量字典
class Momentum(BaseOptimizer):

    def __init__(self,
                 param_dict: Dict[str, np.ndarray],
                 learning_rate: float,
                 beta: float = 0.9,
                 from_scratch=False) -> None:
        super().__init__(param_dict, learning_rate)
        self.beta = beta
        self.grad_dict = deepcopy(self.param_dict)
        if from_scratch:
            self.velocity_dict = deepcopy(self.param_dict)
            for k in self.velocity_dict:
                self.velocity_dict[k] = 0

    def save(self) -> Dict:
        state_dict = super().save()
        state_dict['velocity_dict'] = self.velocity_dict
        return state_dict

    def load(self, state_dict: Dict):
        self.velocity_dict = state_dict.get('velocity_dict', None)
        if self.velocity_dict is None:
            self.velocity_dict = deepcopy(self.param_dict)
            for k in self.velocity_dict:
                self.velocity_dict[k] = 0
        super().load(state_dict)

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.velocity_dict[k] = self.beta * self.velocity_dict[k] + \
                (1 - self.beta) * self.grad_dict[k]
            self.param_dict[k] -= self.learning_rate * self.velocity_dict[k]

# RMSProp，额外维护了梯度字典、学习率权重、学习率字典以及一个为了防止分母出现0的平滑项self.eps = eps
# 注意这里的correct_param控制的是是否修正指数移动加权平均数，上面简单提到过，只是没说具体做法，这里有兴趣可以看代码
class RMSProp(BaseOptimizer):

    def __init__(self,
                 param_dict: Dict[str, np.ndarray],
                 learning_rate: float,
                 beta: float = 0.9,
                 eps: float = 1e-6,
                 from_scratch=False,
                 correct_param=True) -> None:
        super().__init__(param_dict, learning_rate)
        self.beta = beta
        self.eps = eps
        self.grad_dict = deepcopy(self.param_dict)
        self.correct_param = correct_param
        if from_scratch:
            self.s_dict = deepcopy(self.param_dict)
            for k in self.s_dict:
                self.s_dict[k] = 0

    def save(self) -> Dict:
        state_dict = super().save()
        state_dict['s_dict'] = self.s_dict
        return state_dict

    def load(self, state_dict: Dict):
        self.s_dict = state_dict.get('s_dict', None)
        if self.s_dict is None:
            self.s_dict = deepcopy(self.param_dict)
            for k in self.s_dict:
                self.s_dict[k] = 0
        super().load(state_dict)

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.s_dict[k] = self.beta * self.s_dict[k] + \
                (1 - self.beta) * np.square(self.grad_dict[k])
            if self.correct_param:
                s = self.s_dict[k] / (1 - self.beta**self._num_step)
            else:
                s = self.s_dict[k]
            self.param_dict[k] -= self.learning_rate * self.grad_dict[k] / (
                np.sqrt(s + self.eps))

#Adam，缝
class Adam(BaseOptimizer):

    def __init__(
            self,
            param_dict: Dict[str, np.ndarray],
            learning_rate: float,
            beta1: float = 0.9,
            beta2: float = 0.999,
            eps: float = 1e-8,
            from_scratch=False,
            correct_param=True,
            lr_scheduler: Callable[[float, int], float] = const_lr) -> None:
        super().__init__(param_dict, learning_rate, lr_scheduler)
        self.beta1 = beta1
        self.beta2 = beta2
        self.eps = eps
        self.grad_dict = deepcopy(self.param_dict)
        self.correct_param = correct_param
        if from_scratch:
            self.v_dict = deepcopy(self.param_dict)
            self.s_dict = deepcopy(self.param_dict)
            for k in self.v_dict:
                self.v_dict[k] = 0
                self.s_dict[k] = 0

    def save(self) -> Dict:
        state_dict = super().save()
        state_dict['v_dict'] = self.v_dict
        state_dict['s_dict'] = self.s_dict
        return state_dict

    def load(self, state_dict: Dict):
        self.v_dict = state_dict.get('v_dict', None)
        self.s_dict = state_dict.get('s_dict', None)
        if self.v_dict is None:
            self.v_dict = deepcopy(self.param_dict)
            for k in self.v_dict:
                self.v_dict[k] = 0
        if self.s_dict is None:
            self.s_dict = deepcopy(self.param_dict)
            for k in self.s_dict:
                self.s_dict[k] = 0
        super().load(state_dict)

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.v_dict[k] = self.beta1 * self.v_dict[k] + \
                (1 - self.beta1) * self.grad_dict[k]
            self.s_dict[k] = self.beta2 * self.s_dict[k] + \
                (1 - self.beta2) * (self.grad_dict[k] ** 2)
            if self.correct_param:
                v = self.v_dict[k] / (1 - self.beta1**self._num_step)
                s = self.s_dict[k] / (1 - self.beta2**self._num_step)
            else:
                v = self.v_dict[k]
                s = self.s_dict[k]
            self.param_dict[k] -= self.learning_rate * v / (np.sqrt(s) +
                                                            self.eps)

至于学习率衰减，就是使用了一个getter函数调用self.learning_rate获得学习率。构造函数中传入一个衰减策略函数供self.learning_rate调用。例如可以使用双曲线衰减函数

def get_hyperbola_func(decay_rate: float) -> Callable[[float, int], float]:

    def scheduler(learning_rate_zero: float, epoch: int):
        return learning_rate_zero / (1 + epoch * decay_rate)

    return scheduler

根据作者的说法，加上这些优化措施后，分类准确率已经达到了80%，对于这种比较丁真的网络结构来说已经很不错了。

纯路人的博客

快速上手深度学习项目(二)