卷积神经网络

卷积神经网络是计算机视觉领域常用的网络架构。其实前面我们处理猫狗分类也是视觉任务，我们的处理是直接把图片拉平，然后用线性层处理，这么做相当于直接舍弃了像素的位置关系。虽然理论上来说你参数量叠的足够的话，这个位置关系可能也能学出来，但是你直接舍弃一个已知的信息，对于完成任务来说这显然是不够高效的，所以科学家们将卷积引入了视觉任务。

原作者是从参数量的角度说在视觉任务中引入卷积的原因，一张图片平铺为一个向量时，这个向量的长度是很哈人的，哪怕是三通道的224*224的图片，长度也达到了224*224*3=150528，这还只是一个线性层的输入，输出你不能维度很小吧，那这一个线性层得要多少参数呢，所以要优化网络结构，因此引入卷积。

什么是卷积

卷积的科普网络上视频很多，你只要不点进一个搞信号的人做的视频里就行。我这里就用我贫弱的语言描述一下CV里的卷积。下面所说的大小、长度都是以像素（或者说矩阵的元素）为单位的。

在图像处理里进行卷积，首先你得有个窗口，窗口一般是边长为奇数的正方形，通道数和图片的通道数一致，窗口每个像素的位置有一个权重。用这个窗口扫描整张图片，可以理解为从左往右，从上往下，在图像上移动这个窗口，一般是逐像素移动。窗口每扫描一个位置，就将图像上像素和窗口对应位置权重做加权求和，得到一个值。由于是从左往右，从上往下扫描的，扫描得到的值也是有位置关系的，所以扫完整张图像后得到的所有值会组成一个新的单通道矩阵，新矩阵就是该窗口对该图像卷积结果，下图展示了使用3*3窗口对单通道图片卷积的过程

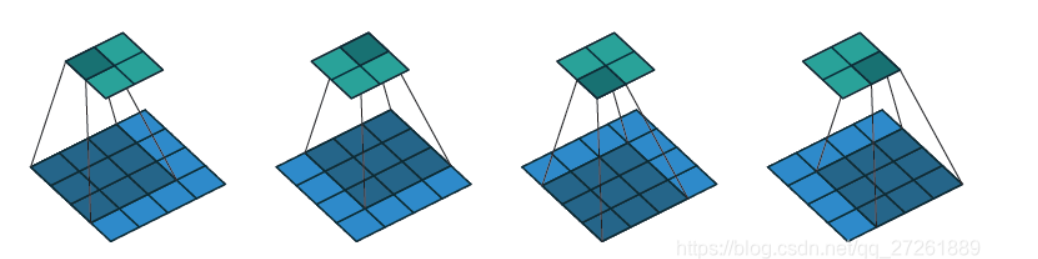
一般来说，我们管这个窗口叫卷积核。需要注意的是，实际上数学中定义的卷积核和上面所说的窗口是中心对称的，这俩并不是一个东西，不过这个细节不重要。下面提几个实际应用卷积层需要注意的点

一个卷积核可以生成一个通道的结果，一个卷积层可以用多个卷积核构成，所以pytorch中创建一个二维卷积层需要的基本参数是输入的通道数（用来确定卷积核通道数）输出的通道数（用来确定卷积数量）和卷积核大小。如上文所说，卷积核一般是3*3正方形，但是它可以是任意规格的矩形。
虽然上面介绍卷积的过程是用卷积核扫描图像，但是稍微想一下就知道这个过程是可以并行的，所以不要怀疑卷积的效率问题。另外卷积结果是源图像多个像素加权求和，显然卷积之后图像的维度是会变的，而且在卷积核扫描的时候如果不是逐像素移动的话，也会影响卷积结果的维度。pytorch中有padding参数和stride参数控制上述的两种行为，padding控制在图像外围补0的行数，stride控制扫描的步长
卷积的本质上是加权求和，这还是个线性操作，自然可以想到我是不是可以加上一个偏置？实际上pytorch默认卷积层就是有偏置的。

在卷积的基础上，下面介绍两个也很常见的操作：池化和反卷积

卷积本质上是将图像划分为一个个感受野，然后在感受野里做加权求和，这个权重就是我们要学习的参数。但是我们是不是只能在感受野里加权求和呢？显然我们还可以直接求平均，求最值，这时就不需要卷积核里的权重了，只要知道一个窗口的大小就行，这种操作我们称为池化(Pool)，执行池化的层叫池化层。池化层不改变通道数
前面说了，如果不设置padding和stride，卷积会将图片越卷越小，像一个下采样的过程，卷积的结果越小一般意味着提取到的特征越精炼，如果是最终结果是为了预测一个数值的话可以直接使用这个精炼特征去预测，但是如果最终是为了生成某种图片的话，比如分割图，或者任务直接就是生成图片的任务，那么就涉及到一个上采样的过程。常规是上采样一般就是插值，但是大部分插值操作都是确定的函数，为了添加可学习的参数，我们可以在插值之后进行一次卷积，这个操作称为反卷积，pytorch中提供了ConvTranspose2d用于反卷积操作，不过反卷积里填充像素操作和一般意义上的插值不同，而是通过卷积操作中的padding和stride两个参数控制的，并且填充的值一般是0，具体怎么控制有兴趣可以自己搜索一下。下图展示了不同插值步长下的两个反卷积过程

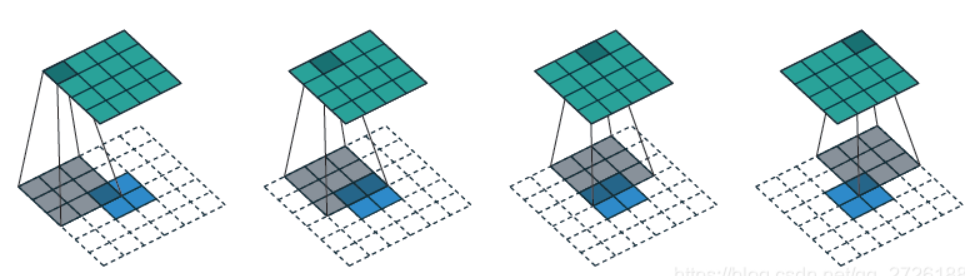
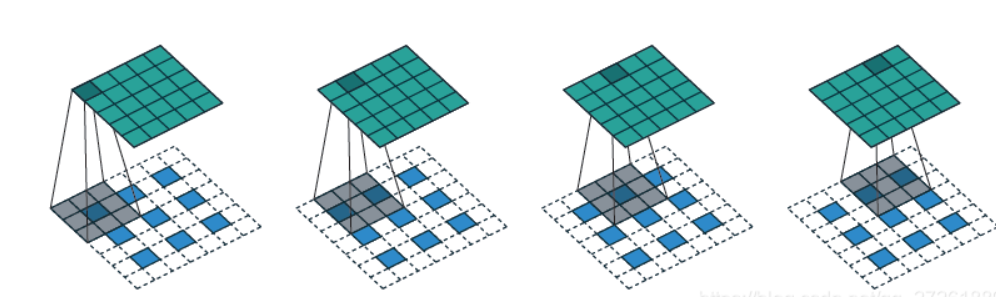
到这里，我们就接触过了线形层（也叫全连接层）、卷积层（这里主要介绍的是二维，一维其实也不难想）、反卷积层（或者叫转置卷积层）、池化层，还有在改进机器学习的基本方法里提到的归一化层，这些层基本就是pytorch里提供的基本神经网络模块。

常见的介绍CV卷积的视频里一般会介绍这么一幅图

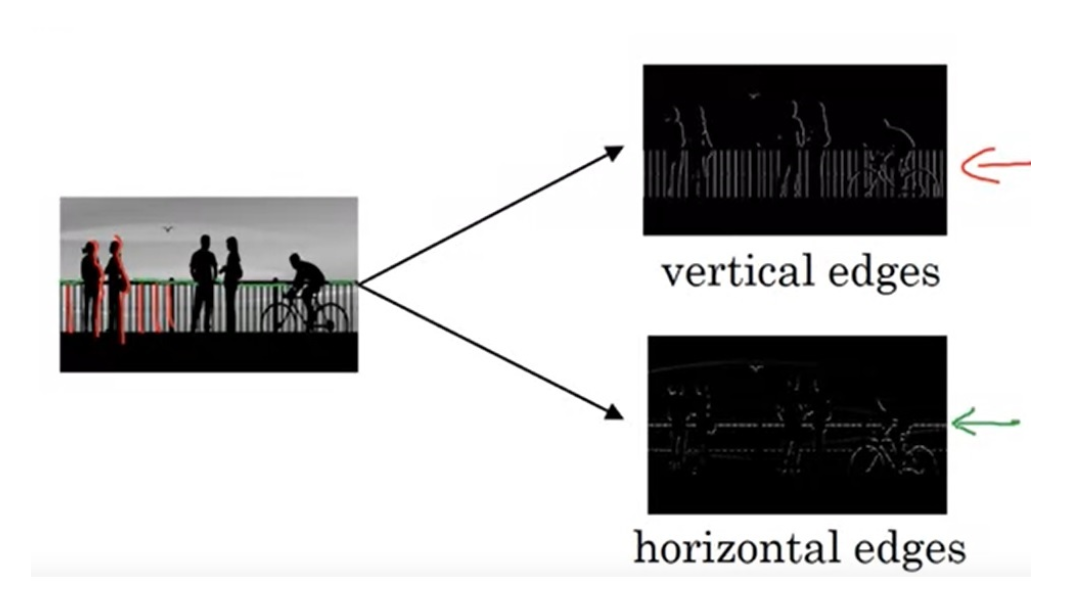
即通过Sobel算子检测水平竖直边缘，传统的数字图像处理介绍这个东西没问题，但是在深度学习里面介绍这个东西，我认为更重要的意义是告诉你卷积可以提取图像特征，而不是让你记住什么样的卷积核可以提取什么样的特征。为什么这么说呢，因为Sobel算子是别人根据傅里叶变换推出来的，是为了提取高频信息而人为设计的，但是卷积神经网络里的卷积核是根据数据学习到的，你不知道他学到的卷积核有什么作用的。虽然我们平时会说图片经过卷积层提取到一层特征，然后怎么怎么处理，好像这个特征是学习到的一样，但实际上神经网络学习的是提取特征的方法，至于提取到的究竟是什么特征，在没有对具体模型逐层分析的时候你不知道提取到了什么特征，你只知道特征很好用就完了。

当然上面的分析也说明了为什么CV领域要引入卷积，因为首先卷积可以针对特定任务提取特定图像特征，并且卷积的得到特征是考虑的空间的拓扑特性的，说明卷积是有效的。此外，一个卷积核对图像每个被扫描到的位置的权重是共享的，而且卷积核的大小也很小，大大减少了参数量，说明了卷积的高效性。卷积神经网络还有很多其他特性，我也记不住，这里懒得说了.。

这里提一嘴，我没有放池化的示意图，因为找到的池化示意图都是步长等于窗口大小的，也就是相当于把图片分块，然后对每个块求统计值（常见的是求最大值，也就是Max-Pooling）。这确实是最常见的，但是容易先入为主，就像有的人一看Sobel算子就无法理解CNN一样，以为CNN里的卷积核也是手动设置的一样。池化本质上还是用窗口去扫描。

常见的CNN架构一般就是首先经过若干个卷积层和池化层，提取精炼特征，然后把精炼特征拉平，送入全连接层进行最后的处理。

pytorch卷积神经网络二分类任务

这里的任务还是之前的猫狗分类任务，不过改用卷积神经网络完成。

首先是数据集处理代码

def load_set(data_path: str, cnt: int, img_shape: Tuple[int, int]):
    cat_dirs = sorted(os.listdir(os.path.join(data_path, 'cats')))
    dog_dirs = sorted(os.listdir(os.path.join(data_path, 'dogs')))
    images = []
    for i, cat_dir in enumerate(cat_dirs):
        if i >= cnt:
            break
        name = os.path.join(data_path, 'cats', cat_dir)
        cat = cv2.imread(name)
        images.append(cat)

    for i, dog_dir in enumerate(dog_dirs):
        if i >= cnt:
            break
        name = os.path.join(data_path, 'dogs', dog_dir)
        dog = cv2.imread(name)
        images.append(dog)

    for i in range(len(images)):
        images[i] = cv2.resize(images[i], img_shape)
        images[i] = images[i].astype(np.float32) / 255.0

    return np.array(images)


def get_cat_set(
        data_root: str,
        img_shape: Tuple[int, int] = (224, 224),
        train_size=1000,
        test_size=200,
        format='nhwc'
) -> Tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray]:

    train_X = load_set(os.path.join(data_root, 'training_set'), train_size,
                       img_shape)
    test_X = load_set(os.path.join(data_root, 'test_set'), test_size,
                      img_shape)

    train_Y = np.array([1] * train_size + [0] * train_size)
    test_Y = np.array([1] * test_size + [0] * test_size)

    if format == 'nhwc':
        return train_X, np.expand_dims(train_Y,
                                       1), test_X, np.expand_dims(test_Y, 1)
    elif format == 'nchw':
        train_X = np.reshape(train_X, (-1, 3, *img_shape))
        test_X = np.reshape(test_X, (-1, 3, *img_shape))
        return train_X, np.expand_dims(train_Y,
                                       1), test_X, np.expand_dims(test_Y, 1)
    else:
        raise NotImplementedError('Format must be "nhwc" or "nchw". ')

load_set没有什么好说的，就是把图片读到一个数组里，对每个图片resize一下并归一化。get_cat_set中里注意两个reshape,opencv读取的图片的shape是(h,w,c)，即通道是最后一维，而pytorch中数据的通道应该是第二维，所以有这个处理，主模块中读取数据的代码应该如下

train_X, train_Y, test_X, test_Y = get_cat_set(
    'path/to/dataset',
    train_size=1500,
    format='nchw')

为什么留了一个nhwc呢，因为原文作者写了两个Tensorflow和pytorch两个版本的代码，Tensorflow中数据的通道数是最后一维。

接下来定义模型

def init_model(device='cpu'):
    model = nn.Sequential(nn.Conv2d(3, 16, 11, 3), nn.BatchNorm2d(16),
                          nn.ReLU(True), nn.MaxPool2d(2, 2),
                          nn.Conv2d(16, 32, 5), nn.BatchNorm2d(32),
                          nn.ReLU(True), nn.MaxPool2d(2, 2),
                          nn.Conv2d(32, 64, 3, padding=1), nn.BatchNorm2d(64),
                          nn.ReLU(True), nn.Conv2d(64, 64, 3),
                          nn.BatchNorm2d(64), nn.ReLU(True),
                          nn.MaxPool2d(2, 2), nn.Flatten(),
                          nn.Linear(3136, 2048), nn.ReLU(True),
                          nn.Linear(2048, 1), nn.Sigmoid()).to(device)

    def weights_init(m):
        if isinstance(m, nn.Conv2d):
            torch.nn.init.xavier_normal_(m.weight)
            m.bias.data.fill_(0)
        elif isinstance(m, nn.BatchNorm2d):
            m.weight.data.normal_(1.0, 0.02)
            m.bias.data.fill_(0)
        elif isinstance(m, nn.Linear):
            torch.nn.init.xavier_normal_(m.weight)
            m.bias.data.fill_(0)

    model.apply(weights_init)

    print(model)
    return model

这段代码我们细说一下。首先nn.Sequential 是 PyTorch 中的一个容器，用来将多个层或操作按顺序组合在一起。它可以让你按顺序执行一系列的神经网络层，而不需要手动定义每个层的 forward 函数调用。这对于结构简单的神经网络模型，或者流水线式的操作特别有用。之前我写的那个pytoch点集分类模型中，我是定义了一个模型，继承自nn.Module，里面有一个forward函数，用for循环遍历每一层。使用nn.Sequential就不需要自定义模型类了，也不需要写forward。不要认为nn.Sequential是什么终极答案，复杂的网络还是要自己写定义模型结构的。

再看具体模型结构，其中涉及到卷积层、归一化层、池化层和全连接层，用到的模块构造函数的所需输入如下

Conv2d: 输入通道数、输出通道数、卷积核边长、步幅、填充个数padding。
BatchNormalization: 输入通道数。
ReLU: 一个bool值inplace。是否使用inplace，就和用a += 1还是a + 1一样，后者会多花一个中间变量来存结果。
MaxPool2d: 卷积核边长、步幅。
Linear（全连接层）：输入通道数、输出通道数。

至于weights_init函数以及model.apply(weights_init)，这是model.apply会递归对每一个nn.Module执行传入的函数。按原博客作者的说法，

由于PyTorch在初始化模块时不能自动初始化参数，我们要手动写上初始化参数的逻辑。

但是实际上pytorch是会对模型参数进行默认初始化的，除非你有特殊的初始化需求，否则没必要这么干。我觉得作者这里应该是搞错了，“由于PyTorch在初始化模块时不能自动初始化参数”这句话的意思应该是模块的构造函数的参数不能自动初始化，而不是模块里的权重矩阵、卷积核、偏置向量等参数不能自动初始化。

使用下面的代码创建模型、优化器和损失函数

model = init_model(device)
optimizer = torch.optim.Adam(model.parameters(), 5e-4)
loss_fn = torch.nn.BCELoss()

训练代码如下

def train(model: nn.Module,
          train_X: np.ndarray,
          train_Y: np.ndarray,
          optimizer: torch.optim.Optimizer,
          loss_fn: nn.Module,
          batch_size: int,
          num_epoch: int,
          device: str = 'cpu'):
    m = train_X.shape[0]
    indices = np.random.permutation(m)
    shuffle_X = train_X[indices, ...]
    shuffle_Y = train_Y[indices, ...]
    num_mini_batch = math.ceil(m / batch_size)
    mini_batch_XYs = []
    for i in range(num_mini_batch):
        if i == num_mini_batch - 1:
            mini_batch_X = shuffle_X[i * batch_size:, ...]
            mini_batch_Y = shuffle_Y[i * batch_size:, ...]
        else:
            mini_batch_X = shuffle_X[i * batch_size:(i + 1) * batch_size, ...]
            mini_batch_Y = shuffle_Y[i * batch_size:(i + 1) * batch_size, ...]
        mini_batch_X = torch.from_numpy(mini_batch_X)
        mini_batch_Y = torch.from_numpy(mini_batch_Y).float()
        mini_batch_XYs.append((mini_batch_X, mini_batch_Y))
    print(f'Num mini-batch: {num_mini_batch}')

    for e in range(num_epoch):
        for mini_batch_X, mini_batch_Y in mini_batch_XYs:
            mini_batch_X = mini_batch_X.to(device)
            mini_batch_Y = mini_batch_Y.to(device)
            mini_batch_Y_hat = model(mini_batch_X)
            loss: torch.Tensor = loss_fn(mini_batch_Y_hat, mini_batch_Y)

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

        print(f'Epoch {e}. loss: {loss}')

训练代码里使用了批处理策略，对于数据的分批就自己看看吧，看不懂说明你切片操作不熟。不过正常情况下我们是使用DataLoader构造batch的，不会像这样写的这么复杂。仔细分析我们会发现传入模型的数据的形状其实是(b,c,h,w)的，实际上pytorch里所有数据都是这个形状的，注意这里的第一个维度是batch，当你在推理时可能只用到一个输入，这时要手动补上batch维度，这就是为什么推理代码里那么多unsqueeze(0)。其他的没什么可说的，loss: torch.Tensor是一个类型注解，不看: torch.Tensor就行，原博客作者真的很喜欢声明类型。

原博客作者还用numpy手搓了卷积的前向过程和反向过程，并且详细介绍了Conv2d的所有参数作用，对卷积过程还是不清楚的同学可以看一下代码。写反向传播的过程作者思路很棒，但是他代码里几乎处理了所有的参数，要考虑的比较多，也不是说有多难，主要是麻烦，看了也记不住。而且他是使用循环扫描的方式实现的，如果bro真的是搞深度学习框架的，面试问你卷积怎么实现，你肯定是用im2col算法然后直接用矩阵乘实现，有兴趣自己去看吧。

深度卷积模型介绍

这一节就沾点科普了，主要介绍几种神经网络。这里主要介绍模型结构，以为如果要魔改（比如你实在没创新点了，硬要往MobileNet里塞Transformer啥的）的话基本就从这里入手。其实除了结构，这些经典网络在诞生时还带火了很多技术，原博客作者说的其实也不很全面，有兴趣可以自己单独搜索。

LeNet-5

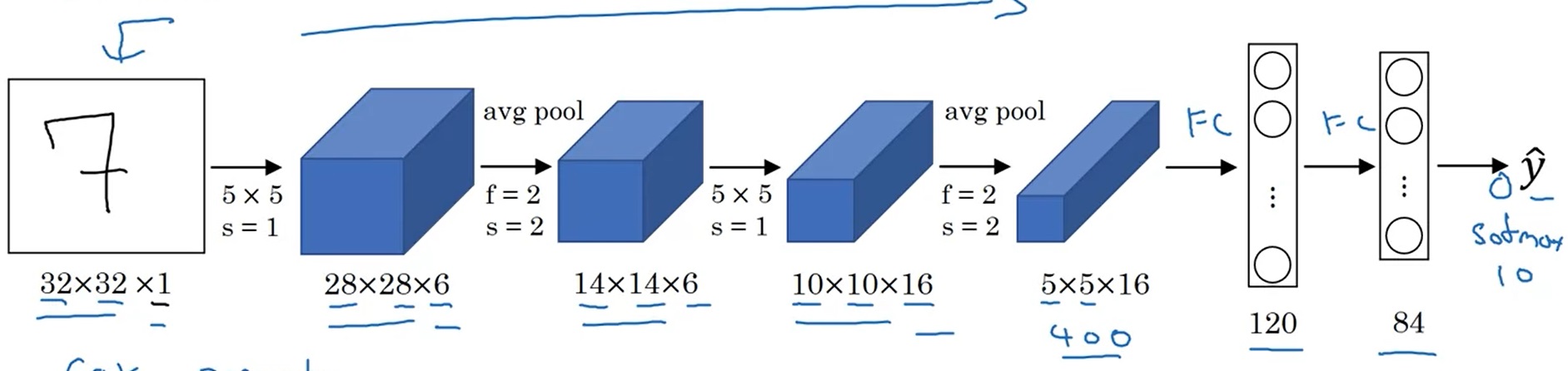
这是1998年提出的一个用于手写数字识别的网络，输入为32*32的灰度图片，经过两个5*5卷积+2*2平均池化后展平输入两个线性层，输出识别的数字，激活函数使用的时softmax和tanh。网络比较拉，但是毕竟经典。

AlexNet

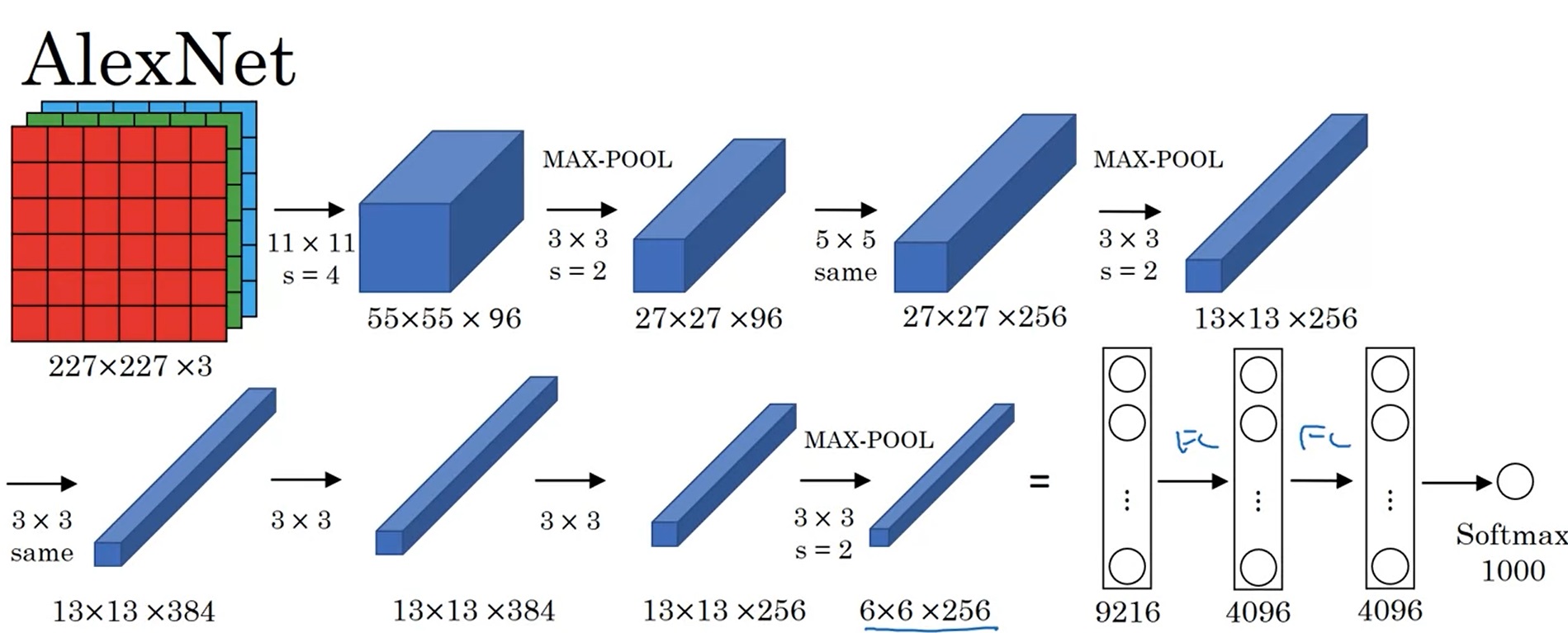
AlexNet是2012年发表的有关图像分类的CNN结构。它的输入是[227, 227, 3]的图像，输出是一个1000类的分类结果。结构也比较简单，总共8层（5个卷积层和3个线性层，5个卷积层里有3个带了池化层）。AlexNet里采用了最大池化，使用ReLU作为激活函数。在工程上AlexNet使用了GPU加速计算，可以说是影响力非常大的工作

VGG-16

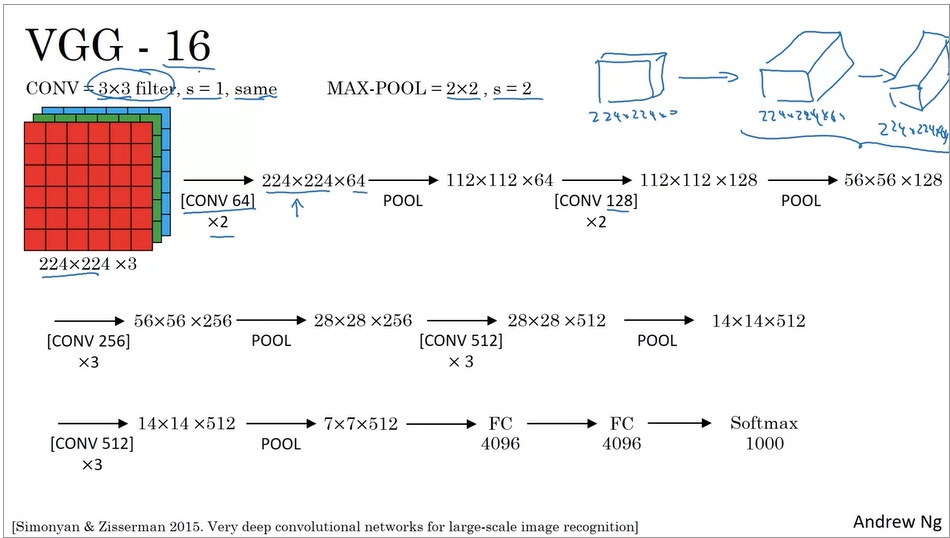
VGG-16也是一个图像分类网络。VGG的出发点是：为了简化网络结构，只用3x3等长(same)卷积和2x2最大池化。VGG是很常用的图像分类CNN，VGG-16指有16层网络，此外还有个VGG-19，这里算层数都是没算池化层的，因为池化层没有参数可以学习的。除了卷积核和池化尺寸之外VGG也没别的，就是深。

ResNets

前面我说VGG已经是很深的网络了，但最多也就19层，再深就面临梯度爆炸/弥散问题了。为了解决这个问题，就需要我们大名鼎鼎的残差结构。残差结构主要就是利用了“跳连(skip connection)”。残差块简单来说就是，假设我们有一个神经网络模块，这个模块可以有多层，具体结构后面分析，其输入为，激活函数为，输出为，正常情况下有

加入跳连后，形成一个残差块,输出变为

当然这样隐含了一个条件，就是和形状相同。不相同时需要使用一个形状变换处理一下

具体到模型结构，下面是ResNet34结构，有34层。

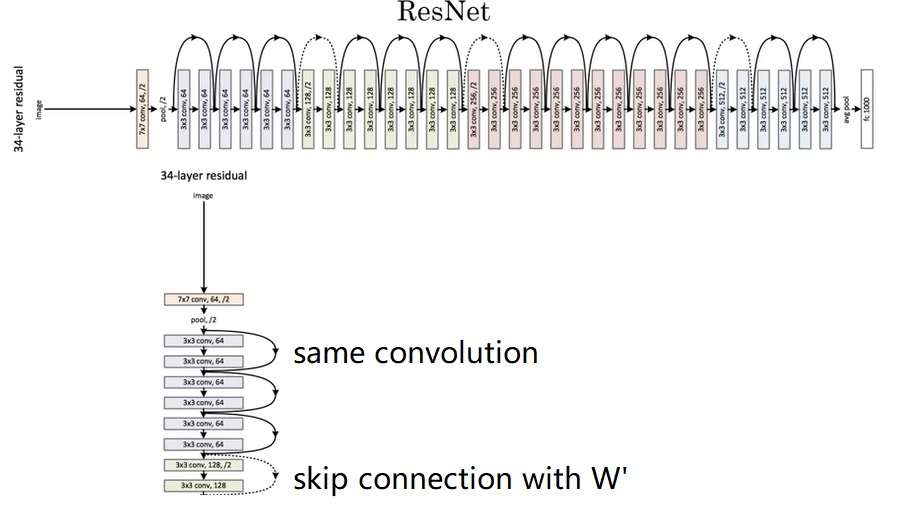
显然一个残差块中的有两层卷积层，其中的虚线意味着需要使用调整形状，是可学习参数。

至于残差块为什么有用，一个通俗理解是加上跳连之后，使用ReLU激活函数，模型至少可以学到一个恒等映射，最起码能够保证较深的网络不比浅的网络差。具体的证明我也懒得看。

Inception 网络

Inception网络由多个Inception块组成，每个Inception块结构如下

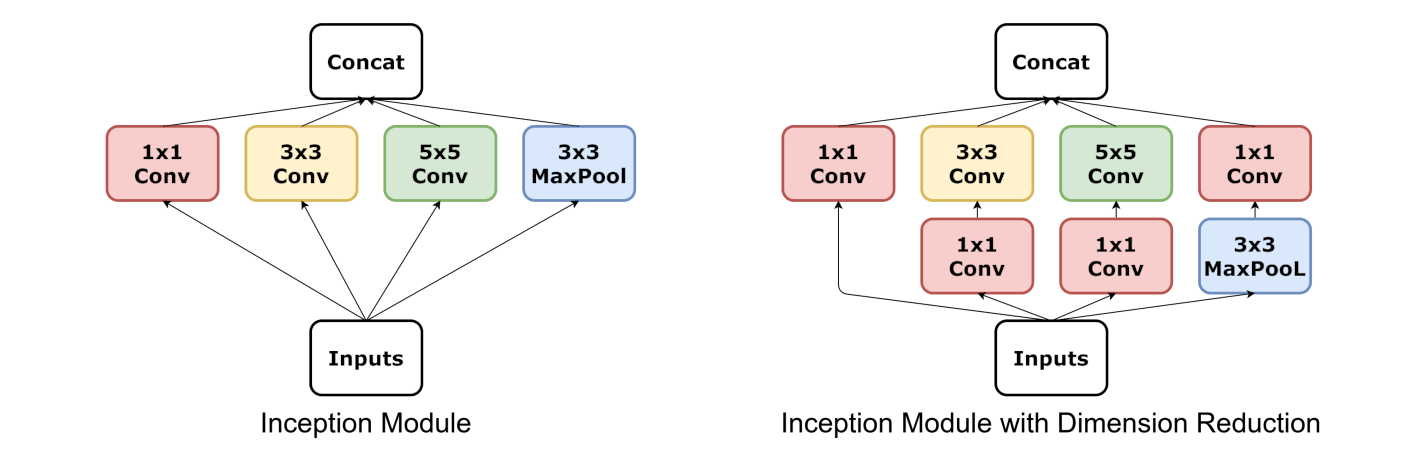
里面涉及到1*1的卷积核，只要记住我前面说的卷积核的数量等于输出通道数，同时理解到卷积核不同通道之间的权重是不共享的（前面说了，通道数和图片的通道数一致，窗口每个像素的位置有一个权重）应该不难理解1*1卷积核主要用于变换图像通道数，比如要把一个192通道数的图像变成32通道的，就应该用32个1x1卷积去卷原图像。

先看左边的Inception模块，所有操作都是通过设置padding从而保持输入大小的，concat操作是在通道维度上进行的。多个大小的卷积核可以提取不同尺度。

右边的Inception模块就是再左边的基础上，使用了多个1*1卷积核先减小了一下通道数，然后再送到3*3和5*5卷积核去卷积，减少参数量。一般用右边的Inception块比较多

总体Inception Net网络如下所示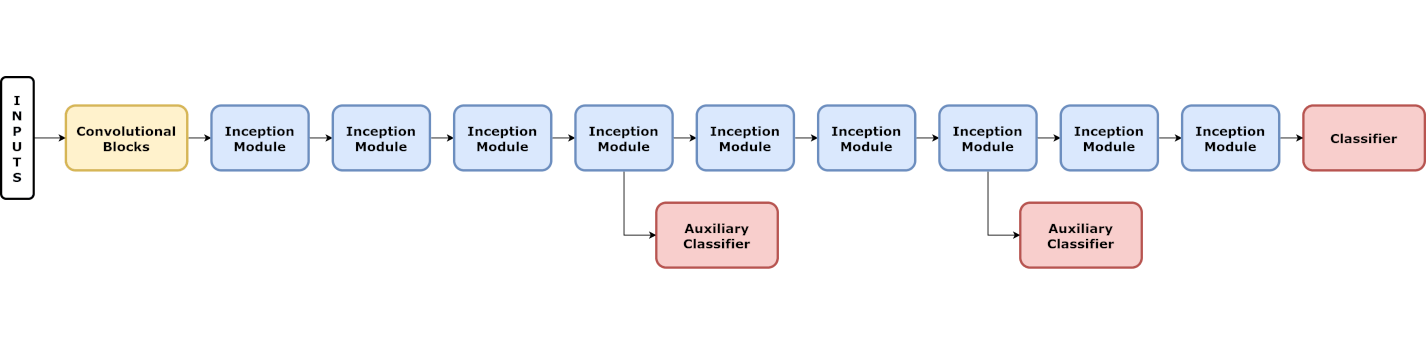

辅助分类器和最终分类器结构一样，都是先池化再1*1卷积降低通道数，然后过两层线性层最后softmax输出。引入辅助分类器主要是为了防止梯度消失和过拟合问题，最初版本的Inception Net是没有残差的，所以在模型的浅层和中层也搞两个输出，这里也是可以算梯度的。

MobileNet

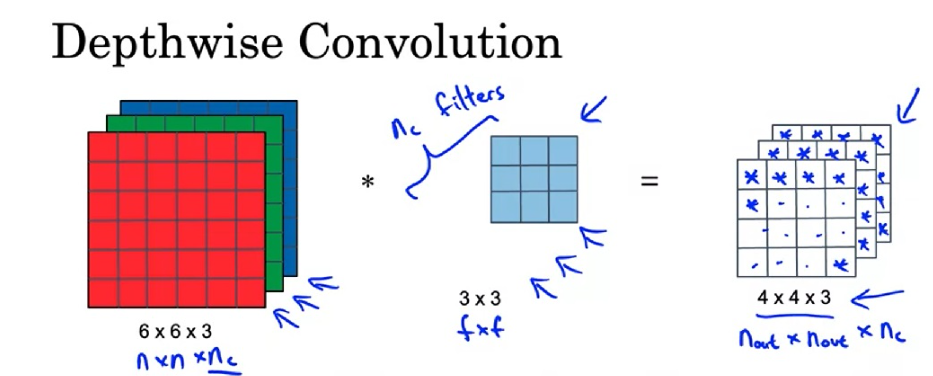
MobileNet由逐深度可分卷积模块组成。传统卷积在一个通道上相当于一个全连接，而逐深度可分卷积(Depthwise Separable Convolution)分为两步：逐深度卷积(depthwise convolution)，逐点卷积(pointwise convolution)。

逐深度卷积生成新的通道，即对于一个多通道的输入，我们把他当作多个单通道输入，使用单通道卷积核对每个通道卷积，最终生成结果的通道数等于输入通道数。这个操作可以通过卷积层的group参数实现，group参数控制按通道分组卷积，默认为1，即所有通道一起参与卷积，而逐深度卷积grounp的值为输入的通道，即每个通道单独成组进行卷积，显然卷积核的通道数应该等于每一组的通道数。

逐点卷积把各通道的信息关联起来。其实就是使用1*1的卷积。

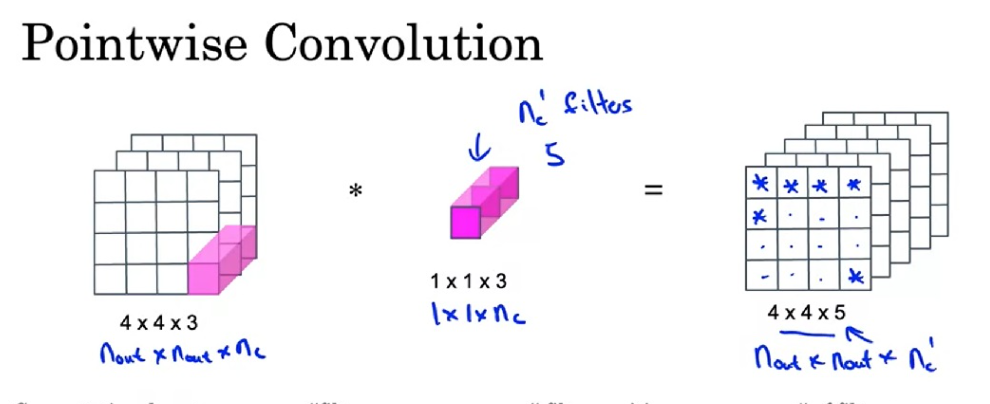
为什么要这么麻烦呢，以为这样可以减少计算量。假设对于一个6*6*3的输入，我们希望使用3*3的卷积核生成5个通道的输出，padding为0，stride为1，我们只算乘法的计算量，就有
$卷积核尺寸卷积核可以移动的位置卷积核数量$
改了之后呢，总计算量变成
$卷积核尺寸卷积核可以移动的位置卷积核数量逐深度卷积卷积核尺寸卷积核位置卷积核数量逐点卷积$
狠狠减少了计算量。

最初始的MobileNet V1就是13个逐深度可分卷积模块堆叠，之后接通常的池化、全连接、softmax。

改进的MobileNet V2加入了残差链接和扩张操作。残差链接不用多说，就是

纯路人的博客

快速上手深度学习项目(四)